1. Introduction

The Gaussian filter is a convolution operator that is used to blur images and remove detail and noise.

In 2D, the Gaussian kernel is described as \(G(x,y)=\frac{1}{2\pi{\sigma^2}}e^{-\frac{x^2+y^2}{2\sigma^2}}\).

Here, \(\sigma\) is the standard deviation of the distribution.

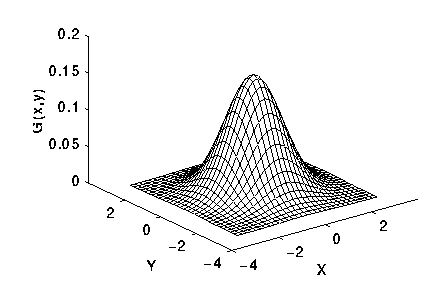
When \(\sigma\) gets larger, the kernel values become smaller. If the kernel size is not increased accordingly, the image gradually becomes darker, as you can see in Video 2 below. To avoid this, the kernel values should be normalized so that their sum is always 1.

The Gaussian filter can be optimized in several ways.

First, in 2D an isotropic Gaussian as shown above is separable into \(x\) and \(y\) components, so the 2D convolution can be computed by filtering in the \(x\) direction and then in the \(y\) direction.

\(G(x,y)=\frac{1}{2\pi{\sigma^2}}e^{-\frac{x^2+y^2}{2\sigma^2}} = \frac{1}{\sqrt{2\pi}{\sigma}}e^{-\frac{x^2}{2\sigma^2}}\cdot{\frac{1}{\sqrt{2\pi}{\sigma}}e^{-\frac{y^2}{2\sigma^2}}}\)

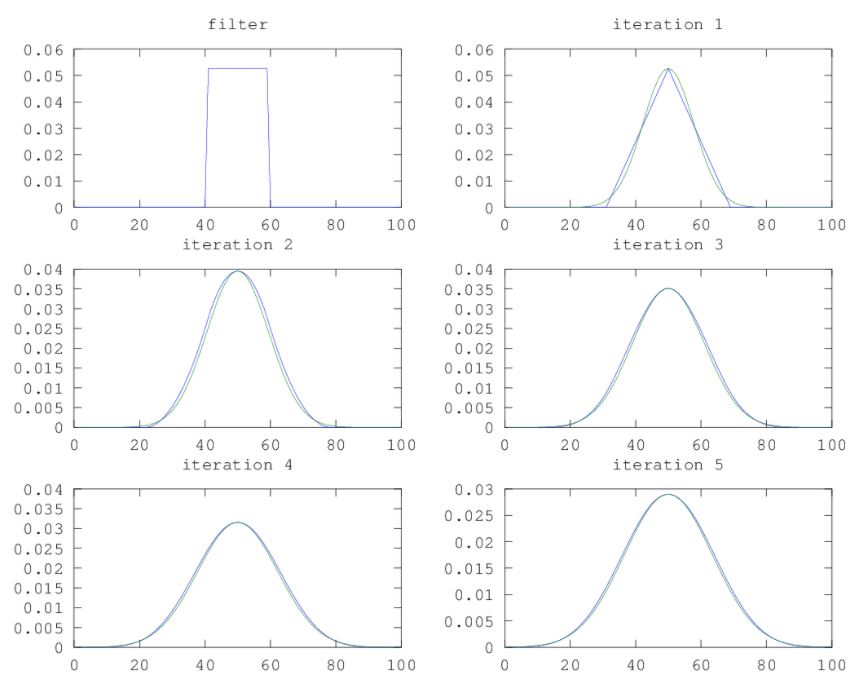
Second, we can approximate a Gaussian using a box (mean) filter. By applying the box filter multiple times, we can obtain an approximate Gaussian filter more efficiently.

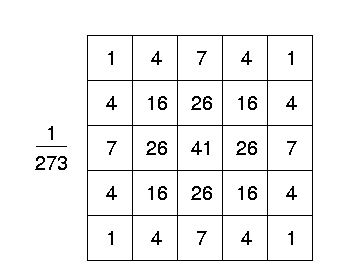
Third, we can use an approximate Gaussian kernel. Below is an approximation of a Gaussian filter with \(kernel\ size = 5\times{5},\sigma=1.0\).

2. Experiment

Video 1: Demo of a 2D Gaussian filter

Video 2: Demo of a 2D Gaussian filter without kernel normalization

3. References

• http://pages.stat.wisc.edu/~mchung/teaching/MIA/reading/diffusion.gaussian.kernel.pdf.pdf
• https://homepages.inf.ed.ac.uk/rbf/HIPR2/gsmooth.htm
• http://elynxsdk.free.fr/ext-docs/Blur/Fast_box_blur.pdf
• http://nghiaho.com/?p=1159